什么是非球面系數?它都有哪些分階?
在相機鏡頭、顯微鏡甚至手機攝像頭中,非球面鏡片(Aspherical Lens)因其優異的像差校正能力被廣泛應用,而賦予非球面鏡片這種能力的核心“密碼”,正是非球面系數。這些看似抽象的數字,實則決定了鏡片表面每一處曲率的微小變化。
一、什么是非球面系數?
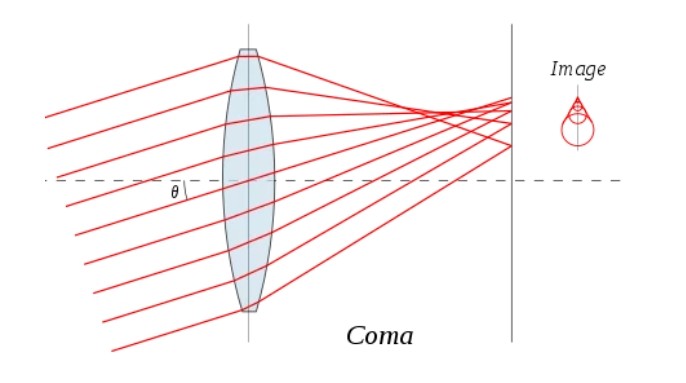
我們都知道,傳統球面透鏡表面是一個均勻彎曲的球面,但光線通過時會產生球差、彗差等像差問題,導致成像模糊或變形。非球面透鏡的曲面尤其非球面的曲率設計,使得它能夠很好優化球差、彗差等像差問題,曲率隨位置變化,能更精準地控制光線路徑。
為了系統性描述非球面這種復雜曲面,科學家在基礎球面形狀上疊加一系列高階修正項,這些修正項的系數就是“非球面系數”,而非球面系數則通過不同階數的組合實現微調鏡片表面,實現消除像差,提升成像質量。
二、非球面系數的分階方式
非球面系數按多項式階數分類,常見的分階方式如下:
偶次非球面多項式(Even Asphere)
最常用的表達式為:
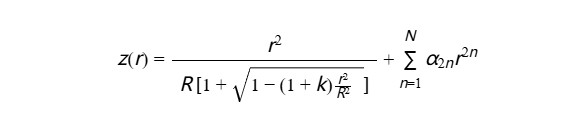
基曲部分:第一項為球面基礎形狀,R為基曲半徑,K 為圓錐常數(描述拋物面、雙曲面等類型)
非球面修正項:為非球面系數,對應 r2n 的階數(如 2階、4階、6階等)。

低階項(如 ):校正低階像差(如離焦)。
高階項(如 ):校正球差、場曲等復雜像差。
更高階項(如 ):用于精密系統的精細調整,但加工難度顯著增加。
Zernike多項式
另一種分階方式基于Zernike多項式,其各項對應不同的像差模式(如第4階為離焦,第5-6階為像散等)。但非球面系數通常更直接關聯偶次多項式模型。
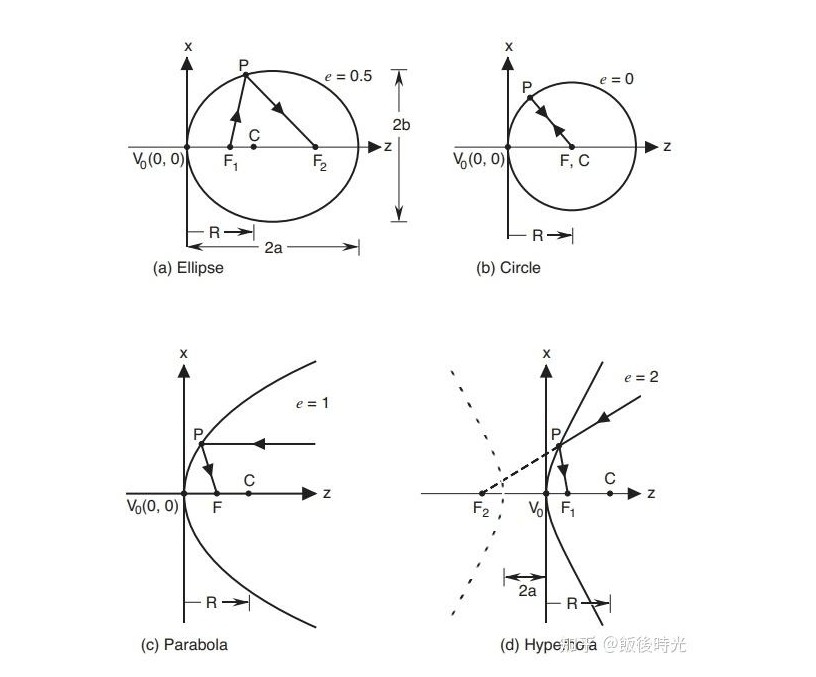
(圖源知乎飯后時光)
三、分階的意義:從普通眼鏡到太空望遠鏡
非球面系數的分階直接決定了鏡片的性能上限:
1. 低階修正(4~6階)
應用場景:普通相機鏡頭、眼鏡片。
特點:成本低,可大幅減少球差和場曲,滿足日常需求。
2. 中高階修正(8~12階)
應用場景:高端顯微物鏡、天文望遠鏡。
特點:通過密集的高階項組合,幾乎消除所有單色像差,但需依賴超精密加工技術(如金剛石車削)。
3. 極限高階(14階以上)
應用場景:極紫外光刻機、太空光學系統。
特點:追求納米級精度,但代價高昂,一片鏡片的加工可能需要數月。

四、設計與制造的博弈
非球面系數并非越多越好,分階背后是光學工程師的權衡藝術:
自由度 vs 成本:高階系數增加設計靈活性,但每增加一階,加工誤差風險指數級上升。
像差校正 vs 系統穩定性:過度依賴高階修正可能導致系統對溫度、裝配誤差極度敏感。
以手機鏡頭為例,通常采用4~8階非球面系數,在性能、體積和成本間找到平衡;而哈勃太空望遠鏡的鏡片則動用超過10階系數,確保在極端環境下的成像清晰度。
非球面系數看似是枯燥的數字,實則是現代光學的“基因代碼”。從4階到16階,每一次分階的突破都推動著成像技術的革新——無論是讓手機攝像頭更輕薄,還是讓人類看清百億光年外的星系。未來,隨著加工技術的進步(如3D打印光學元件),更高階的非球面系數或將解鎖更多顛覆性應用,繼續改寫光學的極限。
文章部分圖片源自網絡分享,僅供參考,侵刪---
